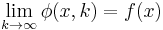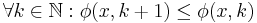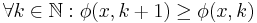Semicomputable function

In computability theory, a semicomputable function is a partial function 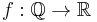$f�: \mathbb{Q} \rightarrow \mathbb{R}$ that can be approximated either from above or from below by a computable function.

More precisely a partial function 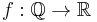$f�: \mathbb{Q} \rightarrow \mathbb{R}$ is upper semicomputable, meaning it can be approximated from above, if there exists a computable function 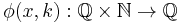$\phi(x,k)�: \mathbb{Q} \times \mathbb{N} \rightarrow \mathbb{Q}$ , where $x$ is the desired parameter for $f(x)$ and $k$ is the level of approximation, such that:

$\lim_{k \rightarrow \infty} \phi(x,k) = f(x)$
$\forall k \in \mathbb{N}�: \phi(x,k%2B1) \leq \phi(x,k)$

Completely analogous a partial function 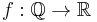$f�: \mathbb{Q} \rightarrow \mathbb{R}$ is lower semicomputable iff 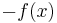$-f(x)$ is upper semicomputable or equivalently if there exists a computable function 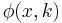$\phi(x,k)$ such that

$\lim_{k \rightarrow \infty} \phi(x,k) = f(x)$
$\forall k \in \mathbb{N}�: \phi(x,k%2B1) \geq \phi(x,k)$

If a partial function is both upper and lower semicomputable it is called computable.

References

Ming Li and Paul Vitányi, An Introduction to Kolmogorov Complexity and Its Applications, pp 37–38, Springer, 1997.

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›

Semicomputable function

See also

References